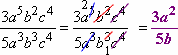Operations withs monomials

Addition and subtraction

We can only add or subtract like monomials; 

• Then we add or subtract the coefficients of the monomials. 

• and put the same literal part (unchanged)

Multiplication

To multiply monomials, 

• we multiply the coefficients (number)
• and then multiply the literal part using the properties of powers (add the exponents of the same variables)

     

Division

To divide monomials, 

• we divide (simplify) the coefficients of the monomials. 
• and then we divide the literal part using the properties of powers (subtract the exponents of the same variables). 

So we obtain another monomial or algebraic expression.

Exercise: Calculate:

a) 3x² + 2x³ + 5x² + 23 - 3x³ + 8 =

b) 3ab³ - 3a³b + 5ba³ - 5b³a + 2ab =

c) (-3ab⁵)·(2a²b³c) =

d) (-12x²y²)·(3x³y⁷) =

e) (7a⁵b³c²):(2a²b²c²) =

f) (15x⁴y⁴):(3x²y⁵) =

Solutions: a) -x³ + 8x² + 31: b) -2ab³ + 2a³b + 2ab; c) -6a³b⁸c; d) -36x⁵y⁹: e) (7/2)a³b; f) 5x²/y

• Simplify 3x + 4x

3x + 4x = 7x 

• Simplify 2x² + 3x – 4 – x² + x + 9

2x² + 3x – 4 – x² + x + 9 
  =  (2x² – x²) + (3x + x) + (–4 + 9) 
  =  x² + 4x + 5
In the second line, many students find it helpful to write in the understood coefficient of 1 in front of variable expressions with no written coefficient, as is shown in red below:
(2x² – x²) + (3x + x) + (–4 + 9) 
  = (2x² – 1x²) + (3x + 1x) + (–4 + 9) 
  = 1x² + 4x + 5 
  =  x² + 4x + 5

It is not required that the understood 1 be written in when simplifying expressions like this, but many students find this technique to be very helpful. Whatever method helps you consistently complete the simplification is the method you should use.

• Simplify 10x³ – 14x² + 3x – 4x³ + 4x – 6
10x³ – 14x² + 3x – 4x³ + 4x – 6 
  =  (10x³ – 4x³) + (–14x²) + (3x + 4x) – 6 
  =  6x³ – 14x² + 7x – 6

• Simplify 25 – (x + 3 – x²)

The first thing I need to do is take the negative through the parentheses:

25 – (x + 3 – x²) 
  =  25 – x – 3 + x² 
  =  x² – x + 25 – 3 
  = x² – x + 22

If it helps you to keep track of the negative sign,
put the understood 1 in front of the parentheses:

25 – (x + 3 – x²) 
  =  25 – 1(x + 3 – x²) 
  =  25 – 1x – 3 + 1x² 
  =  1x² – 1x + 25 – 3 
  =  1x² – 1x + 22 
  = x² – 1x + 22 

• Simplify x + 2(x – [3x – 8] + 3)

x + 2(x – [3x – 8] + 3) 
  =  x + 2(x – 1[3x – 8] + 3) 
  =  x + 2(x – 3x + 8 + 3) 
  =  x + 2(–2x + 11) 
  =  x – 4x + 22 
  =  –3x + 22

• Simplify [(6x – 8) – 2x] – [(12x – 7) – (4x – 5)]

I'll work from the inside out:

[(6x – 8) – 2x] – [(12x – 7) – (4x – 5)] 
  =  [6x – 8 – 2x] – [12x – 7 – 4x + 5] 
  =  [4x – 8] – [8x – 2] 
  =  4x – 8 – 8x + 2 
  =  –4x – 6

• Simplify –4y – [3x + (3y – 2x + {2y – 7} ) – 4x + 5]
–4y – [3x + (3y – 2x + {2y – 7} ) - 4x + 5] 
  =  –4y – [3x + (3y – 2x + 2y – 7) - 4x + 5] 
  =  –4y – [3x + (–2x + 5y – 7) – 4x + 5] 
  =  –4y – [3x – 2x + 5y – 7 – 4x + 5] 
  =  –4y – [3x – 2x – 4x + 5y – 7 + 5] 
  =  –4y – [–3x + 5y – 2] 
  =  –4y + 3x – 5y + 2 
  =  3x – 4y – 5y + 2 
  =  3x – 9y + 2

• Simplify the following expression:

Don't forget that the "5" and the "3" are just numbers. Since 3 doesn't go evenly into 5, I can't cancel the numbers. Don't try to subtract the numbers, because the 5 and the 3 in the
fraction " ⁵/₃ " are not at all the same as the 5 and the 3 in rational expression " x⁵ / x³ ". The ⁵/₃ stays as it is.
For the variables, I have two extra copies of x on top, so the answer is: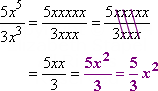

• Simplify the following expression:


I can cancel off the common factor of 5 in the number part of the fraction:





Now I need to look at each of the variables. How many extra of each do I have, and where are they? I have two extra a's on top. I have one extra b underneath. And I have the same number of c's top and bottom, so they cancel off entirely. This gives me: