To multiply a monomial by an addition, we use the distribute property;
Example:
3·( x + 2) = 3·x + 3·2 = 3x + 6
2x·(x + 1) = 2x·x + 2x·1 = 2x2 + 2x
To multiply a polynomial by a monomial, we have to multiply the monomial by each monomial in the polynomial (distribute property)
(5x3 – 3x2 + 1) · 2x2 = (5x3 · 2x2) – (3x2 · 2x2) +(1 · 2x2) = 10x5 – 6x4 + 2x2
... common factor;
To multiply two polynomials, we have to multiply each monomial in one polynomial by the other polynomial.
(5x3 – 3x2 + 1) · (2x2 + 3) = (5x3 · 2x2) – (3x2 · 2x2) + (1 · 2x2) + (5x3 · 3) -(3x2 · 3) + (1 · 3) =
=10x5 – 6x4 + 2x2 +15x3 – 9x2 + 3 =
=10x5 – 6x4 + 2x2 +15x3 – 9x2 + 3 =
= 10x5 – 6x4 +15x3 – 7x2 +3
Vertically;

- Simplify (5x2)(–2x3) I've already done this type of multiplication when I was first learning about exponents, negative numbers, and variables. I'll just apply the rules I already know:
(5x2)(–2x3) = –10x5
The next step up in complexity is a one-term polynomial times a multi-term polynomial. For example:
- Simplify –3x(4x2 – x + 10)
- To do this, I have to distribute the –3x through the parentheses:
- –3x(4x2 – x + 10) = –3x(4x2) – 3x(–x) – 3x(10) = –12x3 + 3x2 – 30x
The next step up is a two-term polynomial times a two-term polynomial. This is the simplest of the "multi-term times multi-term" cases. There are actually three ways to do this. Since this is one of the most common polynomial multiplications that you will be doing, I'll spend a fair amount of time on this.
- Simplify (x + 3)(x + 2)
- The first way I can do this is "horizontally"; in this case, however, I'll have to distribute twice, taking each of the terms in the first parentheses "through" each of the terms in the second parentheses:
- (x + 3)(x + 2) = (x + 3)(x) + (x + 3)(2)
- = x(x) + 3(x) + x(2) + 3(2)
- = x2 + 3x + 2x + 6 = x2 + 5x + 6
This is probably the most difficult and error-prone way to do this multiplication. The "vertical" method is much simpler. First, think back to when you were first learning about multiplication. When you did small numbers, it was simplest to work horizontally, as I did in the first two polynomial examples above:
- 3 · 4 = 12
But when you got to larger numbers, you stacked the numbers vertically and, working from right to left, took one digit at a time from the lower number and multiplied it, right to left, across the top number. For each digit in the lower number, you formed a row underneath, stepping the rows off to the left as you worked from digit to digit in the lower number. Then you added down.
For instance, you would probably not want to try to multiply 121 by 32 horizontally, but it's easy when you do it vertically:
You can multiply polynomials in this same manner, so here's the same exercise as above, but done "vertically" this time:
- Simplify (x + 3)(x + 2)
- I need to be sure to do my work very neatly.
| I'll set up the multiplication: |
| ...and then I'll multiply: | 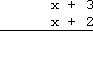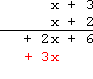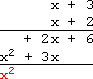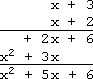 |
- I get the same answer as before: x2 + 5x + 6
Sometimes you will have to multiply one multi-term polynomial by another multi-term polynomial. You can do this horizontally if you want, but there is so much room for error that I usually switch over to vertical multiplication once the polynomials get big. For bigger multiplications, vertical is usually faster, and is much more likely to give you a correct answer.
- Simplify (4x2 – 4x– 7)(x + 3)
- Here's what it looks like when done horizontally:
- (4x2 – 4x – 7)(x + 3) = (4x2 – 4x – 7)(x) + (4x2 – 4x – 7)(3) = 4x2(x) – 4x(x) – 7(x) + 4x2(3) – 4x(3) – 7(3) = 4x3 – 4x2 – 7x + 12x2 – 12x – 21 = 4x3 – 4x2 + 12x2 – 7x – 12x – 21 = 4x3 + 8x2 – 19x – 21
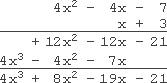
- Simplify (x + 2)(x3 + 3x2 + 4x – 17)
- I'm just going to do this one vertically. Note that, since order doesn't matter for multiplication, you can still put the "x + 2" polynomial on the bottom for vertical multiplication, just as you always put the smaller number on the bottom when you were doing regular vertical multiplication with just plain numbers.
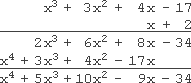
- Simplify (3x2 – 9x + 5)(2x2 + 4x – 7)
- I'll take my time, and do my work neatly:
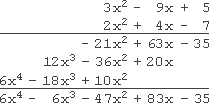
- Simplify (x3 + 2x2 + 4)(2x3 + x + 1)
- Notice that these polynomials have "gaps" in their terms. The first polynomial has an x3 term, an x2 term, and a constant term, but no x term; and the second polynomial has an x3 term, an xterm, and a constant term, but no x2 term. When I do the vertical multiplication, I will need to leave spaces in my set-up, corresponding to the "gaps" in the degrees of the polynomials' terms, because I will almost certainly need the space.
(This is similar to using zeroes as "place holders" in regular numbers. You might have a thousands digit of 3, a hundreds digit of 2, and a units digit of 5, so you'd put a 0 in for the tens digits, creating the number 3,205.)
- Here's what I mean:
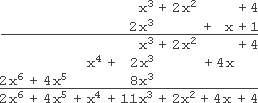
The answer is: 2x6 + 4x5 + x4 + 11x3 + 2x2 + 4x + 4
