To add polynomials, we only have to add their monomials.
Example:
- Add the following polynomials ( 3x3 + 3x2 – 4x + 5) + (x3 – 2x2 + x – 4)
- I can add horizontally:
- (3x3 + 3x2 – 4x + 5) + (x3 – 2x2 + x – 4)
= 3x3 + 3x2 – 4x + 5 + x3 – 2x2 + x – 4
= 3x3 + x3 + 3x2 – 2x2 – 4x + x + 5 – 4
= 4x3 + 1x2 – 3x + 1
Note that each column in the vertical addition above contains only one degree of x: the first column was the x3 column, the second column was the x2 column, the third column was the x column, and the fourth column was the constants column. This is analogous to having a thousands column, a hundreds column, a tens column, and a ones column when doing strictly-numerical addition.
The format you use, horizontal or vertical, is a matter of taste (unless the instructions explicitly tell you otherwise). Given a choice, you should use whichever format that you're more comfortable and successful with. Note that, for simple additions, horizontal addition (so you don't have to rewrite the problem) is probably simplest, but, once the polynomials get complicated, vertical is probably safest bet (so you don't "drop", or lose, terms and minus signs).
- Simplify (2x + 5y) + (3x – 2y)
- I'll put each variable in its own column; in this case, the first column will be the x-column, and the second column will be the y-column:
- Simplify (7x2 – x – 4) + (x2 – 2x – 3) + (–2x2 + 3x + 5)
- It's perfectly okay to have to add three or more polynomials at once. I'll just go slowly and do each step throroughly, and it should work out right.
Adding horizontally:
- (7x2 – x – 4) + (x2 – 2x – 3) + (–2x2 + 3x + 5)
= 7x2 – x – 4 + x2 – 2x – 3 + –2x2 + 3x + 5
= 7x2 + 1x2 – 2x2 – 1x – 2x + 3x – 4 – 3 + 5
= 8x2 – 2x2 – 3x + 3x – 7 + 5
= 6x2 – 2
Note the 1's in the third line. Any time you have a variable without a coefficient, there is an "understood" 1 as the coefficient. If you find it helpful to write that 1 in, then do so.
- Adding vertically:
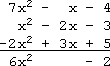
- Simplify (x3 + 5x2 – 2x) + (x3 + 3x – 6) + (–2x2 + x – 2)
- Horizontally:
- (x3 + 5x2 – 2x) + (x3 + 3x – 6) + (–2x2 + x – 2)
= x3 + 5x2 – 2x + x3 + 3x – 6 + –2x2 + x – 2
= x3 + x3 + 5x2 – 2x2 – 2x + 3x + x – 6 – 2
= 2x3 + 3x2 + 2x – 8
When you add large numbers, there are sometimes zeroes in the numbers, such as:
The zeroes in "1002" stand for "zero hundreds" and "zero tens". They are what is called "placeholders", indicating that there are no hundreds or tens. If you didn't include those zeroes in the numerical expression, you'd have just in the top line "12", which isn't what you mean. The zeroes keep things lined up properly. When you vertically add polynomials that skip some of the degrees of x, you need to leave gaps, so the terms line up properly.
- Vertically:
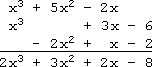
Subtracting polynomials works pretty much the same way....